चार्ल्स एफ. विल्सन की खींची इस फोटो में श्रीनिवास रामानुजन बीच में और उनके गुरू जी. एच. हार्डी तस्वीर में सबसे दायीं तरफ हैं।

बात 1919 की है जब श्रीनिवास रामानुजन लंदन में थे। उनके मित्र और गुरू, जी. एच. हार्डी उनसे मिलने एक टैक्सी से गये। उस टैक्सी का नंबर था 1729। बातों बातों में उन्होंने रामानुजन को बताया, “मेरी टैक्सी का नंबर बड़ा साधारण था। यह किसी बुरे वक्त का संकेत तो नहीं”। “नहीं बिल्कुल नहीं”, रामानुजन बोले, “यह कोई साधारण संख्या नहीं। यह सबसे छोटी संख्या है, जो बनती है दो संख्याओं के घनों को जोड़कर, दो अलग-अलग तरीकों से।”

आइये, हम भी कंप्यूटर के साथ बातों-बातों में ऐसी ही खास संख्याएं ढूंढें।

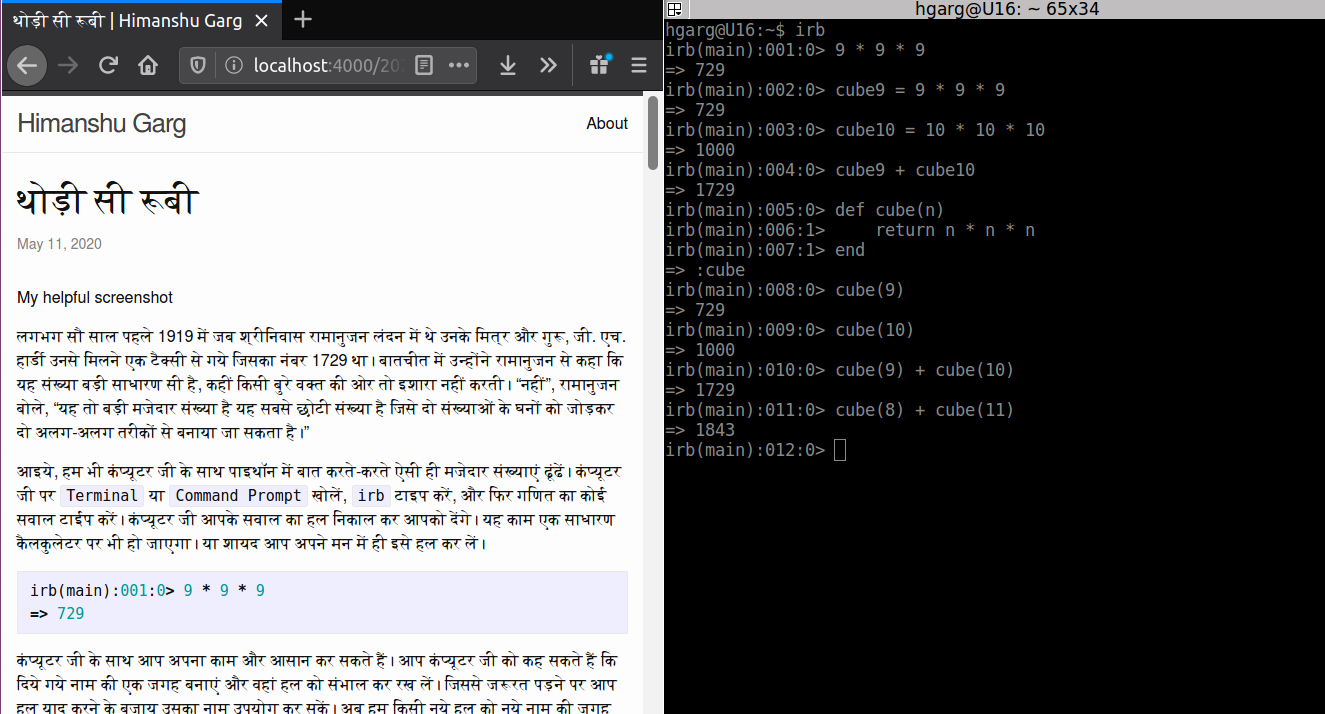
कंप्यूटर पर Terminal या Command Prompt खोलें, irb टाइप करें, और फिर गणित का कोई सवाल टाईप करें।

> 9 * 9 * 9
=> 729

> 10 * 10 * 10
=> 1000

> 9 * 9 * 9 + 10 * 10 * 10
=> 1729

कंप्यूटर के साथ हम अपनी खोज और भी आसान कर सकते हैं। हम संख्याओं को नाम दे सकते हैं और फिर उन संख्याओं को याद करने के बजाय उनका नाम ले सकते हैं। यह नाम चर कहलाते हैं।

> cube9 = 729
=> 729

> cube10 = 1000
=> 1000

> cube9 + cube10 
=> 1729

> cube10 - cube9
=> 271

हम संख्याओं को नाम देने के साथ-साथ उन्हें बनाने के तरीके को भी नाम दे सकते हैं। और फिर कंप्यूटर को काम का पूरा तरीका बार-बार बताने के बजाय, बस तरीके का नाम ही ले सकते हैं। तरीकों को दिये गये नाम फलन कहलाते हैं।

> def cube(n) 
>     return n * n * n
> end
=> :cube
> cube(9)
=> 729

> cube(10)
=> 1000

> cube(9) + cube(10)
=> 1729

> cube(8) + cube(11)
=> 1843

> cube(cube(10))
=> 1000000

• क्या और कोई संख्याऐं हैं जिन्हें cube(?) + cube(?) करने पर 1729 आता हो? कुछ अलग-अलग संख्याओं के साथ आज़माएं यदि 1729 आ जाये?

  > cube(7) + cube(12)
  

• sumCubes नाम का एक फलन बनाएं जो दो संख्याओं को खुद से तीन बार गुणा करके जोड़कर बताए।

  def sumCubes(a, b)
    ?
  end
  > sumCubes(2, 3)
  => 35
  

कोई संख्या खास है कि नहीं यह पता करने का काम अभी भी हमें ही करना पड़ रहा है। इसके बजाय हम कंप्यूटर को बता सकते हैं कि कैसे पता लगाएं कि कोई संख्या खास है कि नहीं। जिससे वो खुद पता लगा कर अलग-अलग स्थिति में अलग-अलग काम कर सकें।

> if cube(12) + cube(1) == 1729
>     puts("sum of 12 cubed and 1 cubed is 1729")
=> nil

> if cube(13) + cube(0) != 1729
>     puts("13 cubed is not 1729")
> else
>     puts("13 cubed is 1729")
13 cubed is not 1729
=> nil

• checkSumOfCubes नाम का एक फलन बनाएं जो दी गई दो संख्याओं के घनों को जोड़ कर बताए कि 1729 आता है या नहीं।

  >>> def checkSumOfCubes(a, b)
  ...     if ?
  ...         true
  ...     else
  ...         false
  >>> checkSumOfCubes(1, 11)
  true
  >>> checkSumOfCubes(2, 10)
  false
  

किसी काम को बार-बार कराने के लिये हम उस काम को बार-बार बता सकते हैं।

> puts("जय हो!")
जय हो!
=> nil

> puts("जय हो!")
जय हो!
=> nil

> puts("जय हो!")
जय हो!
=> nil

या कंप्यूटर को कह सकते हैं कि उस एक काम को बार-बार करते रहें।

> while true
>     puts("जय हो")
> end

• इसको चला कर देखें क्या होता है।

  > n = 0
  > n = n+1
  > puts(n)
  > n = n+1
  > puts(n)
  

• पिछले सवाल में जो काम बार-बार हो रहा है उसे while से कैसे कराएंगे?

  > n = 0
  > while true
  >   ?
  > end
  

• इस सवाल में जो काम बार-बार हो रहा है उसे while से कैसे कराएंगे?

  > n = 0
  > product = 1
  > n = n+1
  > product = product * 10
  > puts(n)
  10 
  > n = n+1
  > product = product * 10
  > puts(n)
  100
  

किसी काम को हमेशा के लिये करते रहने के बजाय हम कंप्यूटर को कह सकते हैं कि काम को वापस करने से पहले जांच कर लें कि काम को आगे करना भी है या नहीं।

> n = 0
> while n < 10
>     puts n
>     n = n+1
> end
0
1
2
3
4
5
6
7
8
9
=> nil

• यदि हमें किसी संख्या को खुद से ही 100 बार गुणा करना हो तो कैसे करेंगे?

एक जैसी बहुत सारी चीज़ों पर कुछ काम करना हो तो सबके अलग-अलग नाम रखने के बजाय हम उन चीज़ों की एक सूची बना सकते हैं। o

> greetings = ["सलाम", "नमस्ते", "हैलो"]
=> ["सलाम", "नमस्ते", "हैलो"]

> fib = [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
=> [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]

>>> puts(names[0])
सलाम
=> nil

> puts(names[1])
नमस्ते
=> nil

> puts(names.length)
3
=> nil

puts(names[names.length - 1])
हैलो

> greetings.push('सत् श्री अकाल')
> greetings.push('सत् श्री अकाल')
> puts(len(greetings));
5
> puts(greetings[3]);
सत् श्री अकाल
> puts(greetings[4]);
सत् श्री अकाल

greetings.each { |item| puts(item) }

> puts(greetings.include('सलाम'))
=> true

> puts(greetings.include('अलविदा'));
=> false

• यदि हमें 1 से 100 तक की संख्याओं की सूची बनानी हो तो कैसे बनाएंगे?
• numbersUpto नाम का एक फलन बनाएं जो 1 से लेकर दी गई संख्या तक की संख्याओं की एक सूची बना कर दे।

  > def numbersUpto(start, finish)
  >     numbers = []
  >     while start <= finish
  >         ?
  >     end
  > end
  > puts(numbersUpto(10))
  

• इसको चला कर देखें क्या आता है।

  >> greetings.forEach(function(item1, index1, array1) {
    greetings.forEach(function(item2, index2, array2) {
        console.log(item1, item2);
    });
  });
  

• पिछले सवाल में कुछ लाईनें आती हैं जिनकी शायद हमें जरूरत ना हो, यदि हमें उनको हटाना हो तो क्या कर सकते हं।

  >> greetings.forEach(function(item1, index1, array1) {
    greetings.forEach(function(item2, index2, array2) {
        if (?) {
            console.log(item1, item2);
        }
    });
  });
  

• 1 से 11 तक की संख्याओं को खुद से तीन बार गुणा करके एक सूची बनाएं।

  >>  let listOfNos = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11];
  >>  let listOfCubes = [];
  >>  listOfNos.forEach(function(item, index, array) {
        listOfCubes.push(?);
    });
  

• getListOfCubes नाम का एक फलन बनाएं जो दी गई संख्या तक की सारी संख्याओं के घनों की एक सूची बना कर दे|

  > def getListOfCubes(n)
  >    ?
  > end
  > list = getListOfCubes(11)
  > puts(list[list.length - 1])
  1729
  

यह एक फलन है जो हमें 9999 तक की सभी ऐसी संख्याएं बता देता है जो 2 संख्याओं के घनों से बनती हैं।

> def taxiNos(list)
    nos = [];
    list.each { |item1| 
        list.each { |item2|
            sum = cube(item1) + cube(item2);
            # यदि sum चार अंकों तक का ही है और अभी तक नहीं मिला है
            if sum <= 9999 and nos.include?(sum) == false
                nos.push(sum)
            end
        }
    }
    return nos
end
> taxiNos(numbersUpto(1, 21))

• Taxicab(n) नाम का एक फलन बनाएं जो वो सबसे छोटी संख्या बताए जो n अलग-अलग तरीकों से 2 संख्याओं के घनों को जोड़कर बनती है।

  > def Taxicab(n)
  >     ?
  => :Taxicab
  > Taxicab(2)
  1729
  

श्रीनिवास रामानुजन ऐसी संख्याऐं बिना कंप्यूटर के आसानी से ढूंढ लेते थे और उनके लिये शायद हर संख्या खास थी। आज वो हमारे बीच तो नहीं, पर हमारे साथ बात करने के लिये कंप्यूटर तो है।

और जानने के लिये हम ये वेबसाईट देख सकते हैं।

• Structure and Interpretation of Computer Programs - https://mitpress.mit.edu/sites/default/files/sicp/full-text/book/book.html

• Ruby Documentation - https://www.ruby-lang.org/en/documentation/

• Taxicab number - https://en.wikipedia.org/wiki/Taxicab_number